The Pascal Distribution is a fairly commonly-used distribution that represents the number of trials required to produce the kth success in a sequence of Bernoulli trials. It is useful in analyzing and designing games of chance. One example is the number of spins needed to get a win on a slot machine. It has also been used to estimate the distribution on the time for electricity load to reach a certain saturation level
The Pascal Distribution represents the number of coin flips required to produce the kth head in a sequence of flips with a biased coin. The probability of a head on any flip is p. The parameters of the distribution are k, which must be a positive integer, and p. The distribution is:
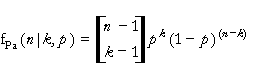
where k=1,2,..., n=k,k+1,..., and 0<p<1.
The equations for the mean and variance are:
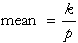
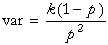
The equations for the parameters are:
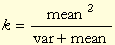
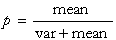
The mean must be positive. Also the expression for k must produce a positive integer.
Versions: DPL Professional, DPL Enterprise, DPL Portfolio
See Also