The Hyperexponential Distribution is based on the Exponential Distribution. In fact, it results from flipping a biased coin to select one of two Exponential Distributions. The coin has probability p of coming up heads, thus selecting an Exponential Distribution with parameter 2*p*lambda. If the coin comes up tails, it selects an Exponential Distribution with parameter 2*(1-p)*lambda. The Hyperexponential Distribution does not commonly apply to a wide range of cases, and thus care must be taken to ensure that the circumstances are appropriate when choosing the Hyperexponential Distribution.
The Hyperexponential Distribution represents a coin flip to select one of two exponential distributions. The two exponential distributions have parameters that depend on the probability, p, of getting a head on the coin flip. The parameters of this distribution are lamda, which must be positive, and p. The distribution is:
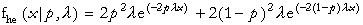
where x>0, 0<p<1, and lamda>0.
The equations for the mean and variance are:
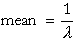
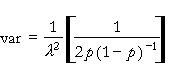
The equations for the parameters are:
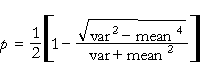
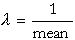
The standard deviation must exceed the mean. Also the mean must be positive.
Versions: DPL Professional, DPL Enterprise, DPL Portfolio
See Also