The Chi-Square Distribution is a subset of the Gamma distribution. It has a number of uses in statistical inference, particularly in cases concerning normal distributions. Some examples are problems of goodness of fit, contingency tables, hypothesis testing and estimation.
The Chi-Square distribution is defined for all positive values of x. It has two parameters, n and sigma, both of which must be positive. In addition, n must be an integer. The distribution is:
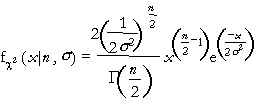
where x>0, n=1,2,..., and sigma>0. The gamma function,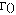 
, is a generalization of the factorial function. Factorials are only defined for integers, but the gamma function can have any number for an argument. If n is an integer, 
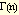= (n-1)!.
The equations for the mean and variance are:
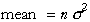
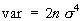
The equations for the parameters are:
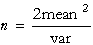
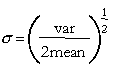
The mean must be positive. Also the expression for n must produce a positive integer.
Versions: DPL Professional, DPL Enterprise, DPL Portfolio
See Also