“…we do not gain all our experience at once, but by degrees; thus our determinations continue to be assailed incessantly by fresh experience; and the mind, if we may use the expression, must always be ‘under arms’.”
-Carl von Clausewitz
Learning Models
Sometimes the uncertainty surrounding a business decision is resolved all at once but most often, uncertainty reveals itself gradually. To find success in today’s business world one must be open to receiving and leveraging relevant information as it comes yet also possess the flexibility to adapt in response. The mathematical representation of this incremental resolution of uncertainty in the decision analysis world is referred to as a learning model.
Most learning models fall into one of two categories:
- Stochastic processes: The prices of certain commodities may follow well known mathematical processes (random walk, mean reverting, etc.)
- Bayesian/subjective learning models: Learning models can be obtained from expert assessments, in much the same way simple probabilities are assessed.
The focus of this post is on the latter, Bayesian learning models, and more specifically the covert feature DPL employs to properly handle the probability data these “true to the world” models at times possess.
Bayesian Learning Models
A Bayesian learning model is useful when there is the opportunity to observe the outcomes of interim uncertainties that will inform you about the outcome of a longer term uncertainty of interest. Two prime examples of this would be a market test that provides information on future sales or near term production results that provides information on the amount of total reserves in an oil or gas field. If the decision to invest in an asset can be delayed or if an incremental investment can be made in the short term, the learning in a Bayesian model can be exploited.
Bayesian Revision
With this type of modelling you will occasionally encounter situations in which you assess conditional probability information one way (e.g., what is the probability that A is high given that B is high) but encounter the events chronologically in the reverse order (i.e., given B is high what is the probability A is high).
With DPL, you’re free to assess the relationship in either order. DPL’s automated bayesian revision feature allows you to specify uncertain relationships the way the data comes to you in the Influence Diagram but model them in the Decision Tree in the order they occur in the real world.
In the figures provided you’ll see that the the input probabilities show that the outcome of the market test is influenced by the actual market results – this relationship may have been ascertained from past data or experience. This matches what is displayed in the Influence Diagram.
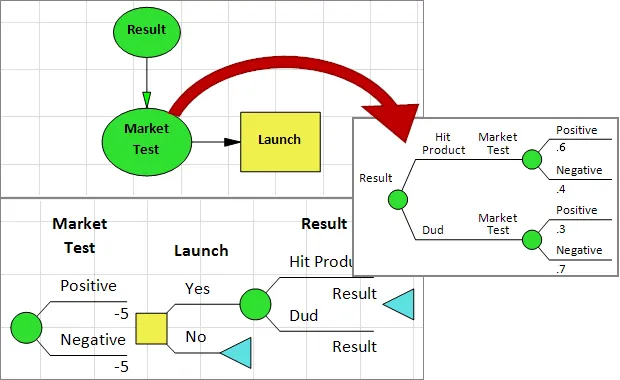
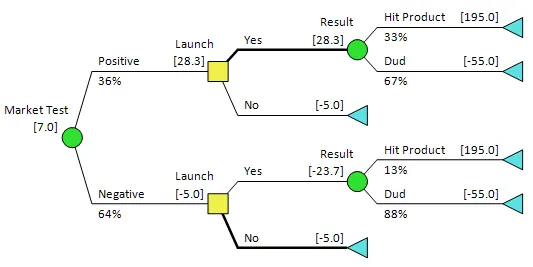
Try it for yourself!
I would encourage you to build a simple learning model in DPL and try the Bayesian Revision feature out for yourself by. To do so you can request a free trial license of DPL 9 Professional via the button below. Take a look at the tutorial contained in Chapter 7 of the DPL 9 User Guide entitled Conditioning and Learning in Decision Models, a PDF for which you can find here. The tutorial will prompt you to open the Learning.da DPL workspace file that is installed with your trial license within the Examples folder of your DPL installation directory (C:\ProgramFiles\Syncopation\DPL9\Examples), you can also download it below.