The PowerBall lottery recently reached a record jackpot – after not having been won since November. Tickets to play the lottery cost $2 each (though there are some multipliers you can add on for a couple extra bucks) and the odds of winning the record-smashing $1.5 Billion jack pot as of yesterday were a minuscule 1 in 292 Million (you can read more about the mathematics behind the lottery in this Wired article here). I’d like to point out that, in addition to the huge jackpot, there are a number of other, much smaller cash prizes that can be won with the overall odds of winning any prize being about 1 in 25.
My husband (and maybe myself, just slightly) got wrapped up in the PowerBall hysteria. He tried a few different methods to increase his odds/winnings. First, he bought just a single plain, vanilla ticket. The next week he jumped into the office pool, the buy-in for which was $10 and the winnings would have been evenly split among 20 colleagues. As a last ditch effort, he bought another single ticket but added a 3x multiplier for an additional $2.
This morning it was announced that there were 3 winning tickets sold, which will divide the large prize 3 ways. After the government takes their cut (which varies by state and whether a lump sum is taken) the “bring home” winnings are no where close to the $1.5B. Even still, it isn’t a quantity to scoff at.
Considering the relatively low risk, meager odds, and huge rewards – I was interested to calculate the expected value of various PowerBall plays. Would the EV increase for multiplier add-ons or buying in to the office pool? How low does the Jackpot have to be to have a negative EV? You can download the DPL models I came up with here: Powerball.da
Here are a couple of highlights:
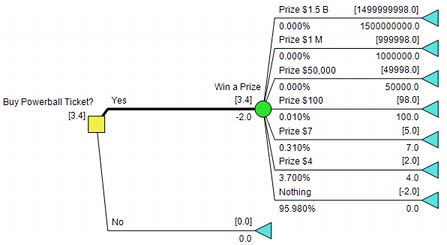 Policy Tree for the decision to buy a Powerball Ticket considering all
prizes
Policy Tree for the decision to buy a Powerball Ticket considering all
prizes
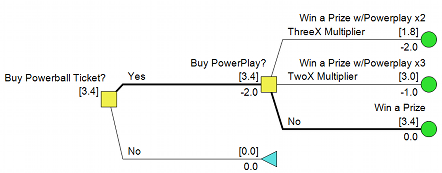 Policy Tree for the decision to add a 2x or 3x multiplier to a Powerball
play
Policy Tree for the decision to add a 2x or 3x multiplier to a Powerball
play
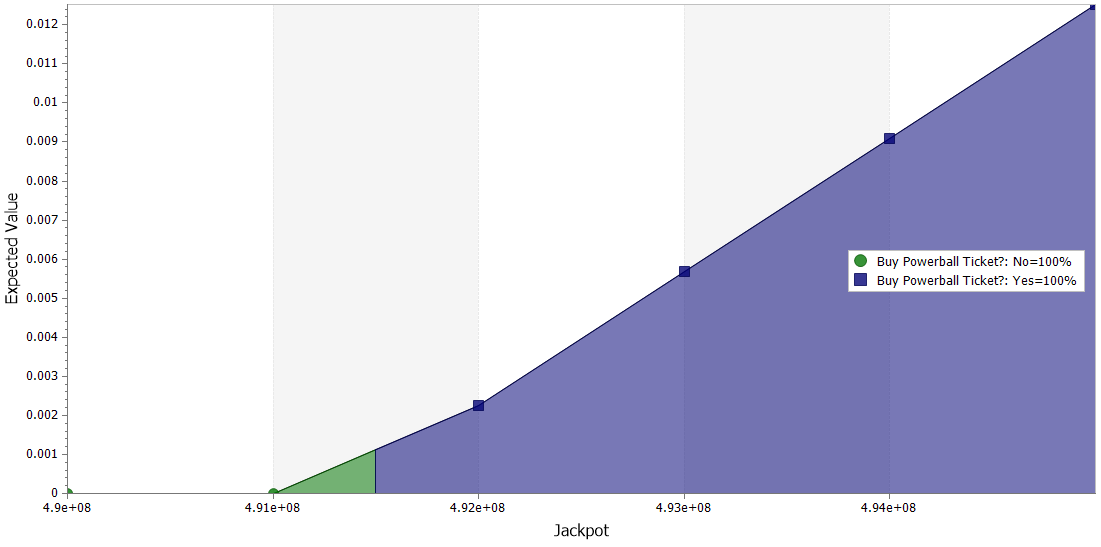
A sensitivity analysis varying the jackpot amount – the optimal policy changes to “don’t buy” if the jackpot is under $491M
One last note – my husband spent a total of $16 on tickets. He ended up winning $12 on the single ticket he’d added the 3x multiplier to. So, not surprisingly, we ended up in the red.
I obtained the odds and prize information via the PowerBall Website: http://www.powerball.com/powerball/pb_prizes.asp