Classic Problem
The Monty Hall Problem
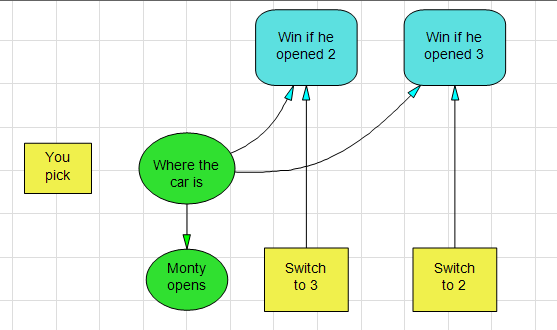
For this classic problem a contestant is presented with three closed doors. Behind one of the doors is a brand new car, while behind the other two doors are goats. After the contestant picks one of the doors, the host, Monty Hall, instructs a stage hand to open one of the other two doors, and behind it lies a goat. Now there are two remaining closed doors, one with a goat and one with a car, and the host gives the contestant the option to switch. Should the contestant switch? Overall, what is the probability that the contestant will win the car?
While this problem sounds simple, it requires subtle reasoning and the answer is counter-intuitive. The key to understanding this problem is capturing the imperfect information revealed by the host opening a door which is best expressed using conditioning in DPL’s Influence Diagram. In the model, the uncertainty for which door he opens is conditioned by the uncertainty for which door the car is actually behind. This is “backwards” from the order they appear in the decision tree, but that’s not a problem, DPL will flip the arcs (Bayesian revision).