When is a Decision Analysis Model Too Simple?

I’m often asked to comment on or critique someone else’s decision analysis model, and I’m actually happy to do so. The space of models is vast, and with each new one there’s always the possibility I’ll discover something truly new, a flavor of uncertainty or unusual approach to capturing it that I’ve never thought about before. (Matter of taste I guess … some people prefer baseball statistics.) Most of the time I’m able to offer suggestions that might improve the model.

As a matter of policy I don’t offer an opinion about whether a model is “correct”. In explaining why not, the analogy I use is that of a map. While there are some maps (and some models) that are glaringly wrong, most are broadly consistent with the facts as known to their author. The question is whether they’re useful for the task at hand. I can draw you a potentially useful napkin-sized map that will tell you how to find the men’s room in the pub down the street (behind the pillar), but if you’re a tax assessor trying to measure the floor area it won’t be at all helpful. In the case of a decision model, understanding that context/need is quite difficult if you haven’t been working with the team all along – is this model improving decision quality or just checking a box?

One of the great things about decision analysis is that you can buy it “by the yard”. A useful DA model can sometimes be hammered out in a few hours, and if the decision is simple and small in impact, that might be the right place to stop. Or, if there’s a lot at stake, and the simplifying assumptions one might like to make are painfully false, an analytical process lasting months might be appropriate. The point to stay focused on is that every step in the direction of more/bigger should be justified based on a reasonable expectation that the added bit will improve decision quality. Some times a 3-4 node model with exhaustively validated inputs is appropriate; other times, only a model that tackles the dynamics will be of any value.

A “Level 1” Model

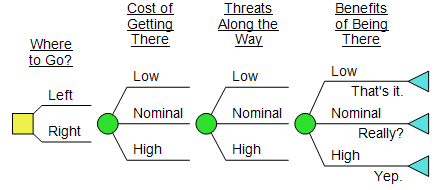
There’s nothing wrong with a Level 1 model, even for a high stakes problem. Again: would adding complexity to the model improve decision quality? If not, spend your analysis budget (literal or figurative) elsewhere. (I’ve heard these models called “Spetzler Specials”, after Carl; he’s been doing this a lot longer than I have so I trust that he spends his analysis budget wisely.)

Next Steps, Or, When is a model Too Simple?

The ways one might improve a Level 1 model are the same as the criticisms one might raise in examining such a model. There are no hard and fast rules. By definition, no model is complete.

A basic model can take you in many directions. Let the preliminary results, as well as your own judgement, suggest areas that need attention. If you do nothing else, take a hard look at the chance node with the highest value of perfect information (VOI) – are you capturing most of its essence? Always remember that complexity is a cost you must pay, not a feature.

These are some possible steps to take/questions to ask:

• Do we have everything? Should we add any more nodes? (This is usually the wrong direction, but it’s what people think of when they hear “more model!”, so I suppose I have to list it.)
• Include one or more downstream decisions (does management really just make that initial decision and retire to the Bahamas?)
• Are all chance nodes modeled symmetrically (life is skewed, especially taxi rides and construction costs)?
• Is there “learning” that we’re ignoring? Do we understand the dynamics of the 1-3 most important (in VOI) uncertainties? (cf. downstream decisions)
• Are all the uncertainties really independent? (This can be huge – if you divide the risk up into a dozen uncorrelated factors – “desktop diversification” – you can fool yourself into thinking the overall risk is much less than it really is.)
• Is this really a single attribute problem? (Are there examples of two outcomes with the same expected NPV that are widely different in terms of intuitive desirability?)
• Is this really a multi attribute problem? (Some models use multiple attributes as a (poor) substitute for tackling the complexities head on – attributes with names like “risk” and “flexibility” are a red flag.)
• Is the optimal decision alternative massively superior? Really? (Delicate point here – sometimes the answer really is obvious once the proper decision frame is determined, but other times you’re making life easy by replacing Pi with 3).

There are more of course, no model (or blog post) is “complete”, but that’s a good first pass. Happy modelling!