How do you tackle a model with 3^18^ paths? Well, whatever you do, you better not do it 3^18^ times! Even if you were able to calculate a billion paths a second, it would still take 30,000 years or so.
The model we recently shared as part of the March Madness promotion was solved using Hybrid Discrete Tree Simulation, one of DPL’s decision tree evaluation methods. As the name implies, discrete tree simulation is a hybrid method that lives in between traditional decision tree rollback and Monte Carlo simulation. It works on a discrete decision tree, but uses sampling to produce an approximate solution without evaluating every endpoint.
When is Hybrid Discrete Tree Simulation best?
Discrete tree simulation is great for discrete decision trees which are very large (generally millions of endpoints or more). Such models may take forever to run using traditional (i.e., Full Enumeration) or even enlightened (Fastest Exact) decision tree rollback methods. Discrete tree simulation with a moderate number of samples (usually some thousands) can often produce a “good enough” answer in a reasonable amount of time.
When is it worst?
Some models just aren’t a good match for discrete tree simulation. There are two main roadblocks you can run into:
- Dark Corners: If your model has a 1 in a billion event with huge consequences, no sampling method is going to give you any joy. For that kind of model, do whatever it takes to make it amenable to an exact method.
- Deep Downstream Decisions: Any sampling method has to do a kind of double take when it gets to a downstream decision. For that decision to be made reasonably, there have to be at least a few samples of each alternative. In DPL, this is called the “restart” parameter (in Home | Run | Monte Carlo Samples). If the model has downstream decisions very deep in the tree, the need to restart the simulation for decent decision policies can negate the speedup of using a simulation method.
It’s worth noting that some models with an absurd number of paths can be evaluated quickly and exactly because of the clever optimizations in DPL’s fastest exact method. The particulars of those optimizations are beyond the scope of this aside, but if your model is suitable, smart exact always beats brute force approximate.
Why not go continuous?
The choice of discrete or continuous is an age old debate in this field, and we at Syncopation are happy to sell arms to both sides. However, it must be said that there is never any speed advantage to moving from discrete to continuous. Anyone who tells you otherwise has pulled a fast one on you, probably by throwing out a few inconvenient downstream decisions.
Tip from the pros: is your model bigger than your problem?
If you have a model with millions of endpoints that takes forever to run, the first thing you should do is see if you can trim it down without losing anything fundamental. There’s a tradeoff here: is it better to evaluate a more realistic problem approximately or a simpler one exactly? As is so often the case in the art of modelling, the answer is “it depends”, but at a minimum you would want to have a decent tornado diagram in hand as you try to answer that question. Most of the time there are at least a few uncertainties with little effect.
How does it work?
The best way to understand discrete tree simulation is to play with it using a small model and a really small number of samples (say 1, 5, 10). What DPL does with those samples is similar to taking a draw from a distribution in continuous Monte Carlo, except that the draws are assigned to existing branches rather than having each sample create its own unique path.
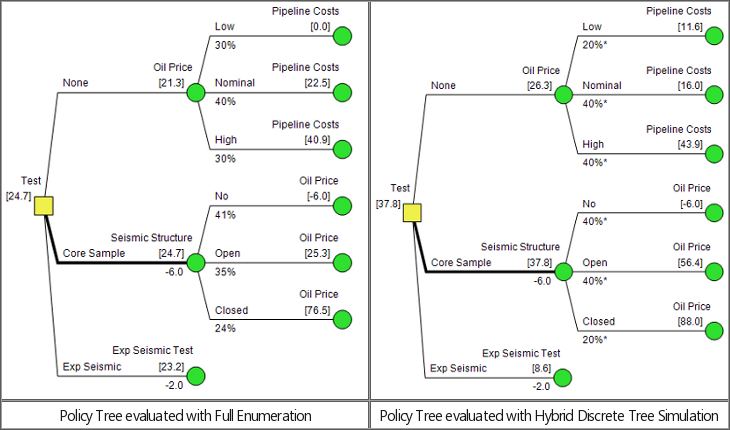
The figures below show the tops of two Policy Trees for a classic
wildcatter problem, one evaluated exactly and one with discrete tree
simulation using five (5) samples (not recommended in real life!).
Simulated probabilities are marked with asterisks. Essentially, “40%*”
in the simulated tree means 2 out of 5 samples.