Decision analysis is most often used on high stakes, one-of-a-kind decisions. However, the same techniques and tools can be used to shed light on a variety of decisions, including those where the stakes are, say, “A BRAND NEW CAR!!!”.
Let’s consider the famous (infamous?) Monty Hall Problem, named for the host of the television game show “Let’s Make a Deal”. In this problem, the contestant is presented with three closed doors. Behind one of the doors is a brand new car. It may only be a Chevy Chevette, but hey, it’s free. Behind the other two doors are goats, which the contestant presumably does not get to take home.
After the contestant picks one of the doors, the host, Monty Hall, instructs a stage hand to open one of the other two doors, and behind it lies a goat. (This is an important assumption – the host never opens the door with the car and laughs, that would be mean.) Now there are two remaining closed doors, one with a goat and one with a car, and the host gives the contestant the option to switch. Should the contestant switch? Overall, what is the probability that the contestant will win the car?
While this problem sounds simple, it requires subtle reasoning and the answer is counter-intuitive. Over the years, many smart people have got it wrong, usually but not always while shooting from the hip.
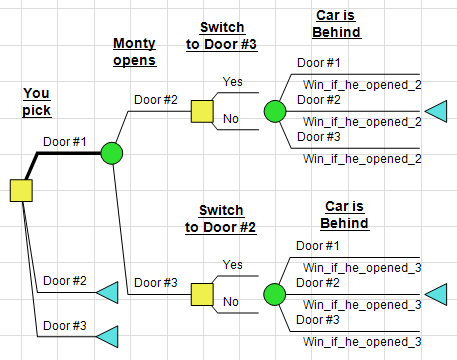
As people who know decision analysis, decision trees, real options and the value of information, we see the option to switch as a downstream decision. Does that downstream decision add value? Well, a necessary condition for it to add value would be for it to be preceded by a revealed uncertainty. We could lay out the decision tree as follows: (In this tree, I’m assuming the contestant’s initial choice is Door #1, since the numbering of the doors is arbitrary.)
Now, does Mr. Hall reveal any decision-relevant information when he opens a door? It’s tempting to say no. Whether or not the initial choice is correct, there will always be a door with a goat for him to open. What then are the odds? If the contestant always sticks with his or her initial choice, the probability of winning is 1/3. However, if she ignores her initial choice and flips a coin to choose one of the two remaining doors, it can’t be worse than 50/50, right?
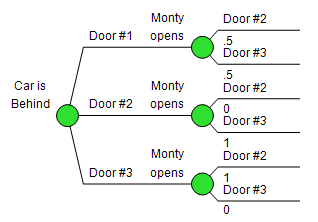
The key to understanding this problem is capturing the (ahem) imperfect information revealed by the host opening a door. We know a few things about that stuff, and it’s often best expressed using conditioning in DPL’s Influence Diagram. In our model, the uncertainty for which door he opens is conditioned by the uncertainty for which door the car is actually behind. This is “backwards” from the order they appear in the decision tree, but that’s not a problem, DPL will do the Bayesian flip without a peep.
As it turns out, if the contestant picks Door #1, and the host opens Door #2, there is a 2/3 chance that the car is behind Door #3. Really! Download the model, doodle on a napkin, or scratch your head, it’s true. Therefore, the contestant should always switch, and the probability of winning is 2/3.
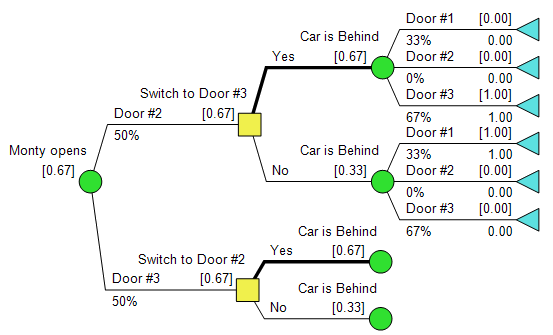
This is a good example of why we at Syncopation are so enthusiastic about the synthesis of Influence Diagrams and Decision Trees, the yin and yang of DA models. While in this case intuition leads first to a tree, without the Influence Diagram thinking of conditioning and Bayesian inference, it would be hard to get this right.