In some sports leagues, particularly those with youth competitors, there is a Mercy Rule by which a game is ended early if one team has built up an insurmountable lead. For example, in little league baseball the rule may be to end the game if one team is ahead 10 runs after 4 or more innings. While the team that’s behind may theoretically have a chance, it’s much more likely that grinding out the rest of the game would only humiliate the losing team and result in everyone getting home late on a school night.
While it isn’t often discussed, most decision consultants employ a kind of Mercy Rule as well. A full scope DA project can be laborious, and if the winning alternative becomes clear, why drag it out?
The downside of declaring a victor early is obvious: what if the preliminary results are misleading and you pick the wrong alternative? However, it’s naive to ignore the downside of continuing a futile analysis. Decision analysts can be quite formal, even pedantic at times. If the results are obvious to the decision makers, and the consultant insists on continuing, the DMs might reasonably conclude that the consultant is more interested in his glorious process (or, gasp, his chargeable hours) than in adding value to the business.
What constitutes an insurmountable lead?
There are times when the answer seems obvious after framing, and I know some practitioners are comfortable calling it at that point. Personally, I’m a numbers guy, and I can’t go that far – there needs to be some quantification before we start talking about winners and losers. However, I’ve been in situations where the apples-to-apples base case NPV’s of the alternatives are so far apart that I and the others on the team were ready to declare after a cursory tornado.
One can always come up with a thought experiment where a “shoot the moon” outcome changes the results in a way that wouldn’t be known without a full probabilistic analysis, but if you’ve framed the problem well and the team includes people experienced in the industry, you should know about any “dark corners” or low probability high impact events.
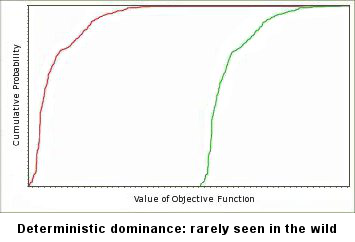
The old school rule: deterministic dominance
If you’ve progressed far enough in probabilistic analysis that you can compare the risk profiles of the competing alternatives of an upfront decision, and the outcome distributions don’t overlap, even the most cautious practitioner would be willing to call it quits. This situation is called deterministic dominance, and is shown in the figure.
There are two problems with deterministic dominance as a rule for shooting the wounded: first, it requires you to do most of the analytical work anyway, and second, rarely are the two distributions totally separate. It’s almost always the case that the upside tail of the “worse” alternative overlaps the downside tail of the “better” one.
A hybrid rule: a biased what-if
One rule I’ve found useful is a kind of biased what-if. It has the advantage that you can check it with only the information required for a standard 10/50/90 tornado diagram. Assuming you’re looking at two alternatives A and B, and preliminary work shows A being better than B, the rule goes like this:
- Set all of the uncertainties specific to A to their pessimistic 10/90 values (i.e., the P10 if it’s a good thing, like revenue, or the P90 if it’s a bad thing, like cost)
- Set all of B’s uncertainties to their optimistic 10/90 values
- Set any uncertainties A and B have in common to their P50’s (be careful: A’s sales and B’s sales are not the same uncertainty!)
- Evaluate the primary metric (e.g., NPV) for both alternatives
- If B is still worse than A, despite all that help, conclude that A > B and terminate the analysis.
Whatever approach you take, make sure you wear your pragmatic hat, and take some responsibility for the decision to terminate or continue. Do you personally have any reasonable doubt about the answer? If not, don’t waste time.