In most DPL models, decisions are made to maximize or minimize some quantity, and they can and should be left unconstrained. You can never have too much NPV, for example. However, some decision problems require making tradeoffs among several decisions where not all possible decision policies (i.e., combinations of decision alternatives) are feasible. For example, your company may only be able to launch one or two new products a year. If your decision problem is all about the constraints, then you’d probably want to approach it with classical optimization methods rather than influence diagrams and decision trees, but a handful of constraints can be easily handled within the context of a DPL decision analysis model.
Consider a simple (and seasonally appropriate) example: I have three desserts in my house, pudding, fruitcake and pie, and I need to decide which of these I’m going to eat. Since this is the holiday season, I’m not limiting myself to one dessert, however I do have a 1000 calorie dessert “budget”. Within that budget I will take as much “satisfaction” (notional units) as I can.
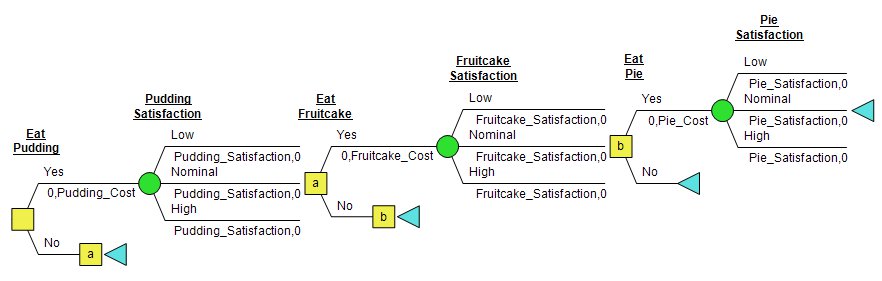
The Decision Tree
My model will have three decisions, each one a yes-or-no for each dessert. The benefits of each dessert are of course uncertain, so the yes branch of each Eat decision is followed by a chance node. I’ve assumed that the decisions are made sequentially (as the desserts make it around the table), although I haven’t modeled any “learning” (does bad pudding beget bad pie? If so I haven’t captured it).
The Attributes
To keep track of my satisfaction and my calories, I’ll use two attributes, Satisfaction and Cost. Through my get/pay expressions, I’ll record the cost of each dessert as I eat it and the satisfaction I gain from it as soon as that uncertainty is resolved. These get/pays can be seen in the tree above.
The Constraint
The constraint is that I cannot exceed my 1000 calorie budget. The “costs” (in calories) of a serving of each of the desserts are coded in three value nodes (Pudding Cost, Fruitcake Cost, Pie Cost), and there is also a Budget value node. To make sure I don’t exceed my budget, I’ve specified objective and constraint functions as shown in the image provided.
The “@if” function is similar to the “=IF” function in Excel, if the first argument is true it returns the second argument, otherwise it returns the third. If on a particular path I exceed my budget, I get “halt(0)”. The halt function is a way of telling DPL not to continue down the path, but to stop right then and there with a fixed value (in this case, zero). I know some paths have positive Satisfaction, so DPL won’t end up choosing a zero value path.
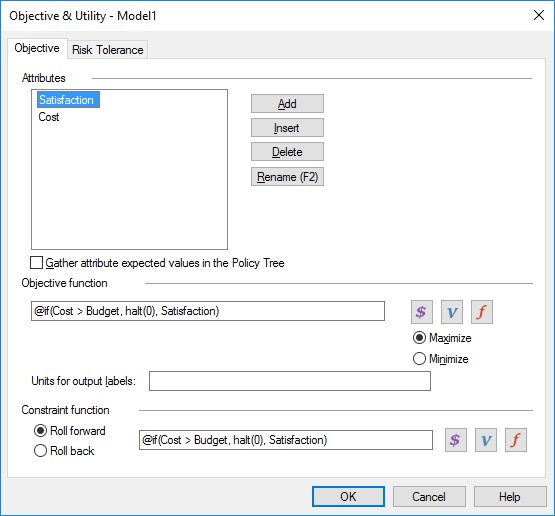
You’ll notice that in this model the objective and constraint functions are the same, which is usually the case. I could have left the constraint function out and got the right answer, but having it makes the evaluation of the tree more efficient because DPL actually “prunes” the Policy Tree, cutting off paths which already violate the constraint. This is a “roll-forward” constraint function. If my constraints were based on rolled back expected values I might need a roll-back constraint function, but that’s a topic for a different post.
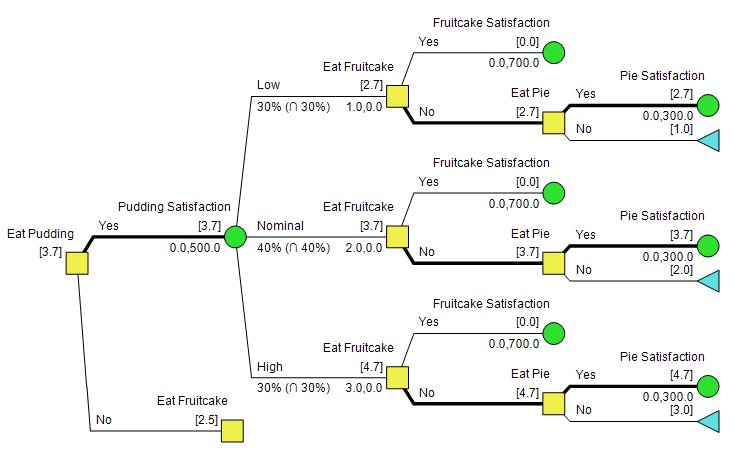
The Results
Running the model, I see that the optimal policy is to eat pudding and pie. This doesn’t surprise me, as a fruitcake always fares poorly in any benefit-cost exercise.
If you’d like to examine this model, you can get it here.
From all of us at Syncopation, we hope your holidays are filled with joy and good cheer! Further, we suggest you enjoy the pleasures of the season without constraints (except possibly where egg nog is concerned).