
(Or, Is this Decision Tree too Chunky?)
When it comes to modelling uncertainty, it seems there are two kinds of people: discrete decision tree people and continuous Monte Carlo simulation people. That’s OK, to a point. Some analyses can be approached with either method, and it is just a matter of taste. But for many problems, one is simply better than the other, and if you choose the wrong one, your analysis is going to be less insightful, or less accurate, than it should be.
Usually, those of us at Syncopation (and most other Decision Analysis oriented shops) find ourselves arguing for a discrete tree approach, against an often ingrained frequentist perspective that smooth curves and results to six decimal places are the key to a good decision (if there even is a decision). But each approach has advantages, and that’s why DPL is happy to go either way.
DPL is Ecumenical
DPL gives you a lot of options for modelling uncertainty, perhaps too many. But fundamentally, DPL is either evaluating a discrete or a continuous model. If you have any continuous chance nodes in your model, you’ll be running a Monte Carlo simulation; otherwise, you have a tree with finitely many paths, and you’ll run some kind of decision tree method.
Now, let me at least nod to a couple of asterisks that complicate that simple taxonomy.
- *1. If you have a discrete chance node and you know that the underlying probability distribution has a specific form and parameters (e.g., that it’s lognormal with mu and sigma 1.7 and 2.6), you can have DPL produce a discrete chance node that appoximates (very well in terms of the moments – I’ll blog the details at some point) that distribution.
- *2. If you have a discrete decision tree with a huge number of paths, you can often evaluate it more quickly by using discrete tree simulation, which basically takes random draws from the decision tree.
In both cases, you’re still working with a fundamentally discrete model.
Why Should you be Discrete?
There are a lot of advantages to a discrete model that you give up when you go continuous. Some of the highlights:
- The Policy Tree. See the “roadmap” of the decision directly. How much does the value of the project go up if we pass that test? It’s right there.
- Direct Conditioning. This is the grab-the-bull-by-the-horns way of dealing with dependence. There are ways of dealing with dependence in a Monte Carlo setting, but they’re opaque and relatively unsatisfying. “If it’s cloudy, the probability of rain is higher.” With direct conditioning, you just make that true.
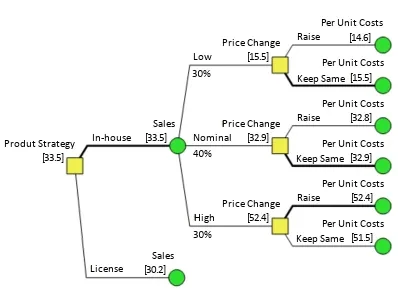
- Results are exact. No random numbers are generated, and if the inputs don’t change, the results are the same from run to run. No need to ponder how many samples are “enough”. (Excepting *2, Discrete Tree Simulation.)
- Downstream Decisions at No Extra Charge. With a discrete tree, a downstream decision is computationally no more difficult than another chance node.
When Should you Go Continuous?
Some of my DA friends might say “when you’re a fool”, but I don’t go that far. There are situations where the structure of the problem makes the “steps” of a discrete tree unacceptable. For example, if you are trying to figure out how often a gas fired power plant will run in a competitive electricity generating system, you’ll need to pay careful attention to its dispatch cost. Say you model gas prices with a single “Low/Nominal/High” chance node, and the plant runs 6000, 1000, or 100 hours respectively. There’s a lot of carpet between 6000 and 1000! If the value model is perfectly linear, you’ll still get the right (expected value) answer, but the messy cash flow spreadsheet converting all those megawatthours to dollars is probably very nonlinear. For a problem with thresholds (triggers, tipping points, etc.), Monte Carlo may be best.
Conclusion
Most of the time, finite is fine, and it’s good to be discrete. But be aware of those thresholds, and by all means play the Monte Carlo card when you need it.