If you have school-age children, you are probably well aware that Saturday is international Pi day. Yes, 3/14/15 bears a passing resemblance to 3.14159265… Now, the skeptics among you will note how weak this resemblance is:
- M/DD/YY is only one of many ways of writing dates (personally, I prefer YYMMDD).
- The calendar is arbitrary in any case.
- Base 10 is arbitrary. Geometry doesn’t care how many fingers you have.
- One can argue that we should have named π/2 instead.
These and other criticisms aside, Pi Day has become a “thing”, and given that it’s at least somewhat educational, one should not object too strongly (although sighing out loud is totally OK). Pi Day is at least as worthy as the average Hallmark holiday.
Now, Pi Day is upon us, and we write about DPL in this blog, so the obvious question is, how to calculate Pi in DPL? The smart-ass answer is, use the intrinsic @pi. OK, that works, but can we calculate Pi the hard way, and will we learn anything by doing so? The answer to both questions is yes.
Series in DPL
In addition to plain old scalar (single value) value nodes, DPL allows you to create one and two dimensional arrays. One dimensional arrays can be defined as series, which just means you will define formulas which apply to ranges of elements rather than having one formula per element.
First a bit of math, it is well known that the series below converges (slowly) to π/4:
1 - 1/3 + 1/5 - 1/7 ...
How to define this in DPL? To keep it tidy, we’ll use three series nodes and one scalar value node. We’ll have one hundred thousand elements in each of our series nodes (I told you it converged slowly), and we’ll number them 1 through 100000. Unlike plain arrays, in a series you can choose your indices (i.e., if you were doing cash flow and not Pi you might want to start with 2015).
The figure shown displays the influence diagram with the data for each node to the right. Let’s focus on odd_ints, and the expression “odd_ints[$-1] + 2”.
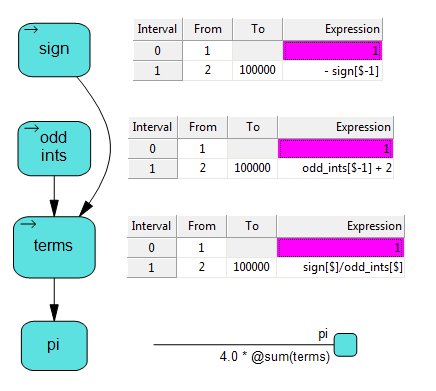
In a DPL series, the dollar sign stands for the subscript of the current element, so [$-1] refers to the previous element. If you think of a spreadsheet, you often have a calculated row in which each element refers to the element immediately to the left, and that’s basically what’s going on here. Each element of odd_ints is two more than the previous one, so starting from 1, we get 1,3,5,7,… etc. The other two series are similar.
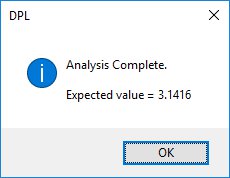
Series calculations in DPL are quite efficient, so 100,000 elements is not a big deal.
When we run the model, DPL calculates all three series, sums up terms in node pi, and reports the results. If you’d like to take a closer look at the model, use the link below:
I hope you’ve enjoyed this bit of light Friday afternoon modelling. Mark your calendars for February 7, 2018!